Computational Statistics, STP 540, Spring 2021

Course Information
Instructor/TA:
Instructor: Robert McCulloch, robert.mcculloch@asu.edu
Office hours (online): Thursdays, 10am
TA: Xiangwei Peng, Xiangwei.Peng@asu.edu
Syllabus
Where we are and what I should be doing?
where and what
Homework
How_to_Submit_Homework_in_Canvas.pdf
Homework 1, Due February 2
Homework 2, Due February 12
Homework 3, Due February 23
Murphy-Kevin_Machine-Learning.pdf
Solution in R for problem 3 on GP
plot of f estimation for problem 3 on GP

Homework 4, Due March 11
Homework 5, Due April 8
Homework 5, R solutions
Discretization and MH for normal data with non-conjugate prior on mean
R and Python
Information on R
Information on Python
Notes
Why are R and Python Slow? Vectorization
Advanced R, Wickham, Section 24.5.
".. vectorization means finding the existing R function that is implemented in C
and most closely applied to your problem."
Simple Logistic Regression, basic notes: Logistic Regression
Simple Logistic Regression: Computing the likelihood, for simple logistic regression.
R code: Logit Example in R
Python code: Logit Example in Python
C++ code:
cmLL.cpp, the C++ code
Makefile, the Makefile to compile C++ code
mLL.R, the R code (which calls the C++ code)
do.R, the R code to show how to use the C++/R code and compare to simple vectorized R
data used in do.R
Rcpp frequently asked questions
looks like a nice webpage for getting started with Rcpp
Calling C++ out of R using rstudio to create an R package
C++ code:
cmll.cpp,
cmll.h,
test.cpp,
Makefile,
test.R,
movie showing how it is done in rstudio
Simple Parallel computing in R
example R script
gettingstartedParallel.pdf
more intense documentation
Simple Parallel computing in Python, thanks Alex!!
demo 1
demo 2
Note:
General GPU on ASU's Research Computing Cluster, February 1, 2021 2:00pm - 3:00pm
This workshop will describe different low and high level approaches to accelerating
existing or developing research codes through the use of Graphical Processing Units (GPUs) on the ASU High Performance Computing cluster.
In preparation for the workshop all attendees are encouraged to
obtain an account
on Agave if they do not already have one.
Register Here.
Matrix Decompositions in Statistics
Quick Review of Some Keys Ideas in Linear Algebra
What Really IS a Matrix Determinant?
QR Matrix Factorization
Least Squares and Computation (with R and C++)
The Multivariate Normal and the Choleski and Eigen Decompositions
Look at cholesky and spectral in R
Singular Value Decomposition
simple example of svd in python
Hi Dr. McCulloch,
In class today you were talking about how in R, the lm() function does a QR decomposition under the hood,
and you were wondering how sklearn's LinearRegression object fits the model.
I was also curious about this, so I took a quick look and wanted to share what I learned.
Quick summary is that it's an SVD under the hood.
Longer summary:
sklearn.LinearRegression calls scipy.linalg.lstsq (
here's the line of code where that happens)
scipy.linalg.lstsq in turn calls one of three LAPACK drivers (
see here).
The default driver is gelsd, which according to
the MKL LAPACK documentation
uses SVD
to solve least squares problems (via Householder transformations, so not entirely unlike the R approach).
So unless you provide sklearn with other constraints (like positive coefficients),
it will by default call a LAPACK routine that solves the least squares problem using SVD.
Best,
Drew
The EM Algorithm
The EM Algorithm
See Chapter 11 of Murphy.
See Chapter 4 of Givens and Hoeting.
See Chapter 8.5 of Hastie, Tibshirani, and Friedman.
Monte Carlo
Monte Carlo
See Chapter 6 of Givens and Hoeting.
Geweke paper
R script to try various truncated normal draws
Rmarkdown version, of R script to try various truncated normal draws
R script to try various importance sampling approaches for prior sensitivity
Rmarkdown version, of R script to try various importance sampling approaches for prior sensitivity
Prior based on odds ratio
SIR R script
Introduction to Bayesian Statistics
Introduction to Bayesian Statistics and the Beta/Bernoulli Inference
Normal Mean Given Standard Deviation
Normal Standard Deviation Given Mean
Multinomial outcomes with the Dirichlet conjugate prior
Introduction to Bayesian Regression
MCMC: Markov Chain Monte Carlo
See Chapter 7 of Givens and Hoeting.
Markov Chains
Simple Example of a Markov Chain
Gibbs Sampling
Gibbs Sampling for hier means
Note: Hoff refers to ``A First Course in Bayesian Statistical Methods'', by Peter Hoff
Reversable Markov Chains
The Metropolis Algorithm
MH example with for normal data with non-conjugate prior on mean
Optimization
Optimization
See chapters 4 and 8 of "Deep Learning" by Goodfellow, Bengio, and Courville.
Lectures
Optimization, Introduction
Gradient and Hessian for Logistic Regression
Taylor's Theorem and Local Minimumaa
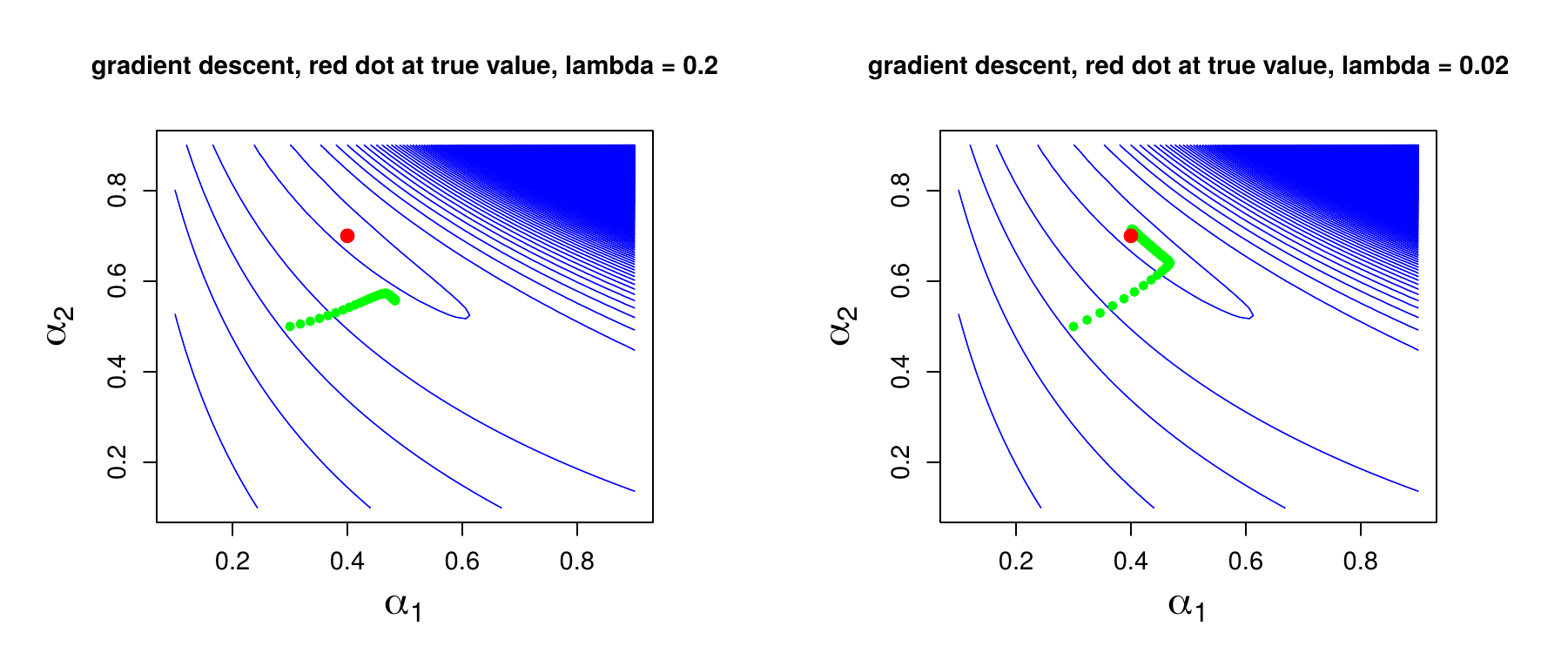
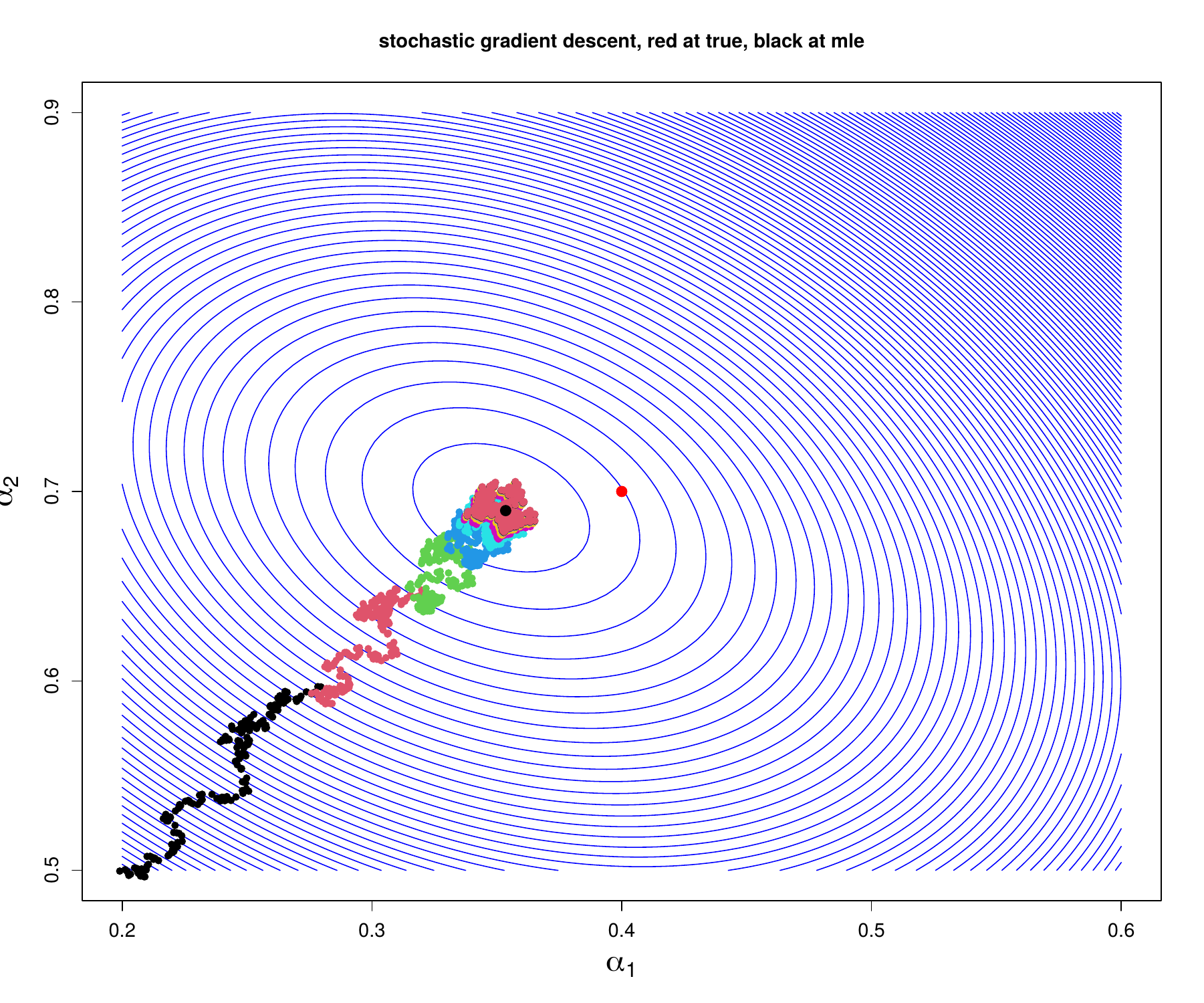
Gradient and Stochastic Gradient Descent
Momentum, RMSprop, and Adam
Newton's Method and Iteratively reweighted least squares
State Space Models and FFBS
Hotels Problem
intro to state space models
FFBS
R code for hotels example
Forward Filtering for Simple Hotels model
The Bootstrap
(Efron and Hastie, chapters 10 and 11)
The Bootstrap
Suggested Projects
Mixture Modeling with EM and MCMC
Details on mixture gibbs sampler
Inference for the parameters of a Gaussian Process
Monte Carlo EM






